Digital Systems and Information¶

Abstract

数字系统：数字信号，典型数字系统。
Digital Systems: Digital signal, typical digital systems
计算机内信息表示法
Information Representation
数制
Number systems
- 进位计数制的概念和十、二、十六、八制数的表示
  Positive radix, positional number systems, decimal, binary, octal and hexadecimal
- 不同进位数制之间的转换
  Conversion Between Bases
编码的概念及带符号二进制数的编码。
Representation for unsigned and signed binary numbers
- 真值、指定长度的机器数：原码、反码、补码。
  Magnitude, Signed-Magnitude, Signed-1’s Complement, Signed-2’s Complement
- 十进制数的二进制编码：BCD 码
  Binary coded decimal (BCD)
- 字符编码：ASCII
  ASCII Character Codes
各种信息的编码
Non-numeric Binary Codes

Digital Systems¶

Types of Digital Systems¶

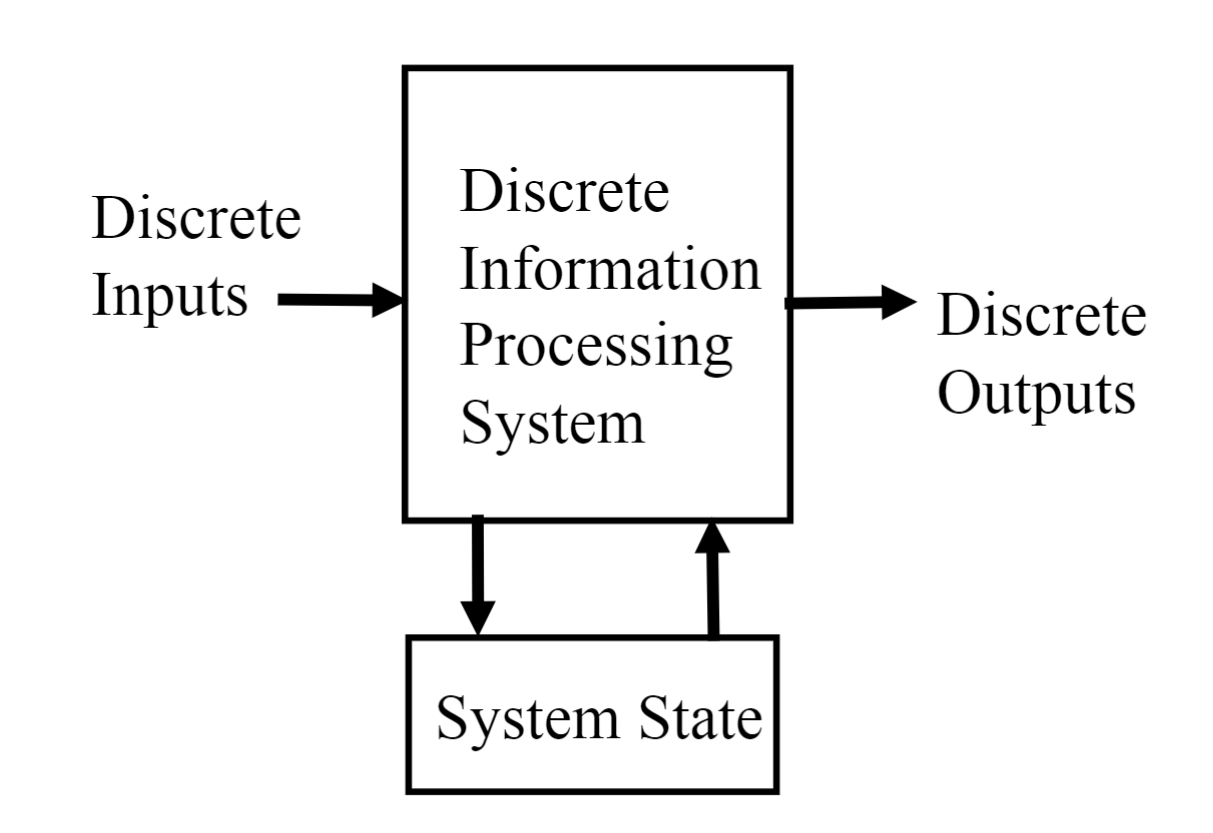
何为“状态”？

董老师：“对于此前若干周期的输入数据的抽象”

有状态后，系统输出必定与当前状态有关

no state present(无状态): Combinational Logic System（组合逻辑系统）：

输入一旦确定，一定有唯一的输出且可预测 / 任意时刻的输出仅取决于该时刻的输入 (output = Function(Input)).
state present(存在状态): Sequential System （时序系统）

任意时刻的输出即取决于该时刻的输入，也取决于电路的当前状态

又分两类：
1. synchronous (同步，按特定周期更新):state update at discrete times
2. asynchronous (异步，无特定周期) :state updated at any time
State = Function(State, Input)
Output = Function(State) or Function(State, Input)

state 不能只和 input 有关吗?

—— 不能, 这样 state 的存在就没有必要了(每次的 state 只是作为了 input 到 output 的中间量.)

Example

汽车上的里程表, 输入 count up 和 reset 信号. 如果 count up 就把里程加一. 输出就是可视化的显式里程. 状态就是里程表的值.
这是非同步的, 因为更新信号的时间不依赖统一时钟, 在任意时刻都可以发生.

Embedded Systems(嵌入式系统)¶

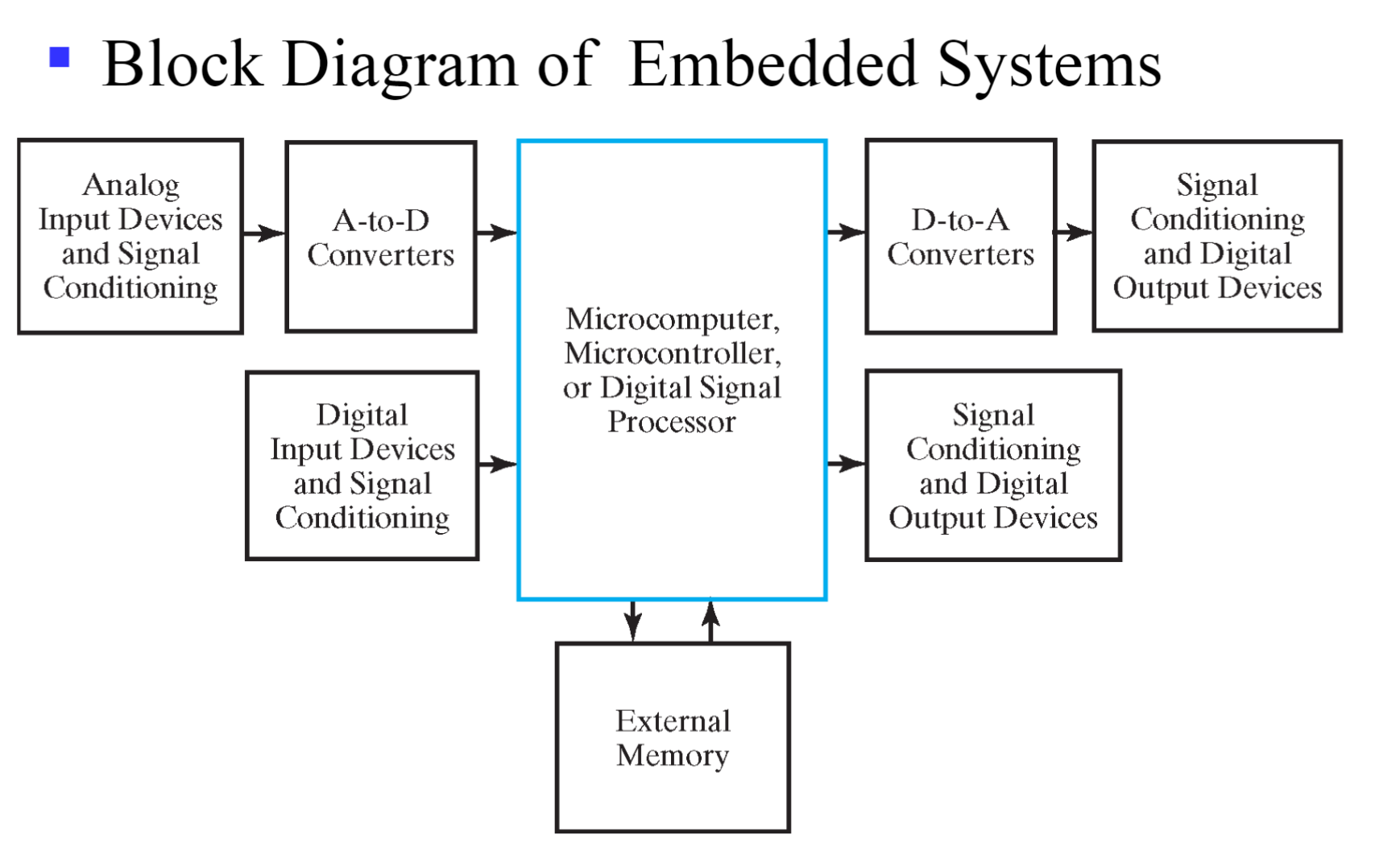
analog input(模拟输入):

A-to-D: 把模拟信号转化为数字信号(处理器不能处理模拟信号)
D-to-A: 处理后把数字信号转化为模拟信号
也有其他的数字输入输出(如按键)

核心: AD & DA, 嵌入式系统区别于日常计算机

A to D

对空调, input 是温度传感器(电阻). 输入是一个电压值, 空调如何理解电压变化?

计算机有以下两个行为:

周期性采样: 采样的周期是由输入信号的信号频率决定.(香农定理确定采样频率)
量化: 按 \(2^n\) 等分数据，使数据离散化(存在误差),n决定采样精度

D to A

DA转换
滤波

Extra

香农定理：采样频率至少在原信号频率的两倍以上

Information Representation¶

Binary values are represented abstractly by:

digits 0 and 1
words (symbols) False (F) and True (T)
words (symbols) Low (L) and High (H)
and words On and Off.

Binary values are represented by values or ranges of values of physical quantities

信号的分类:

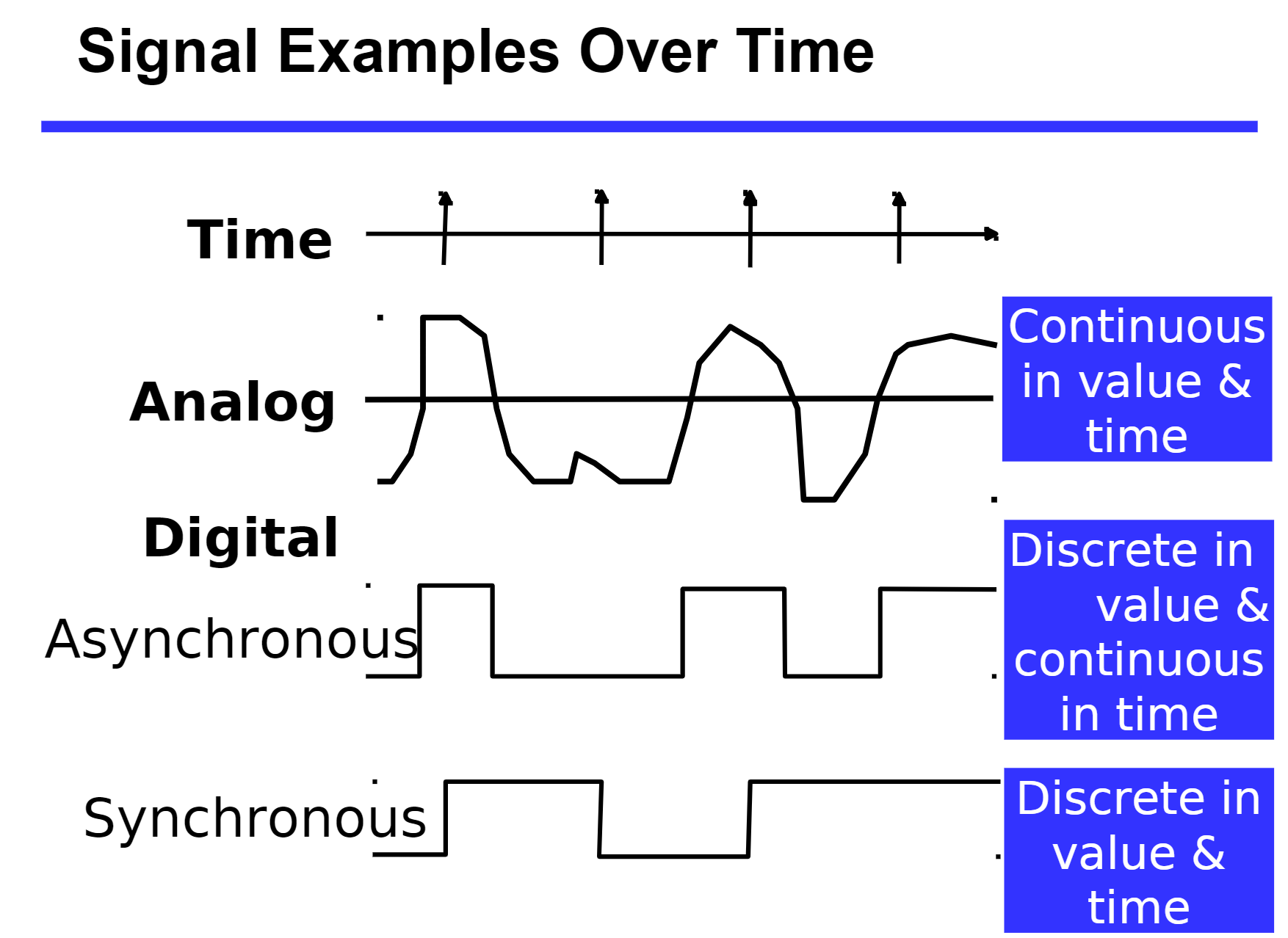
为什么选择二进制数值表示? ---更好对抗数据传输中的干扰
连续信号在传输过程中难免衰减

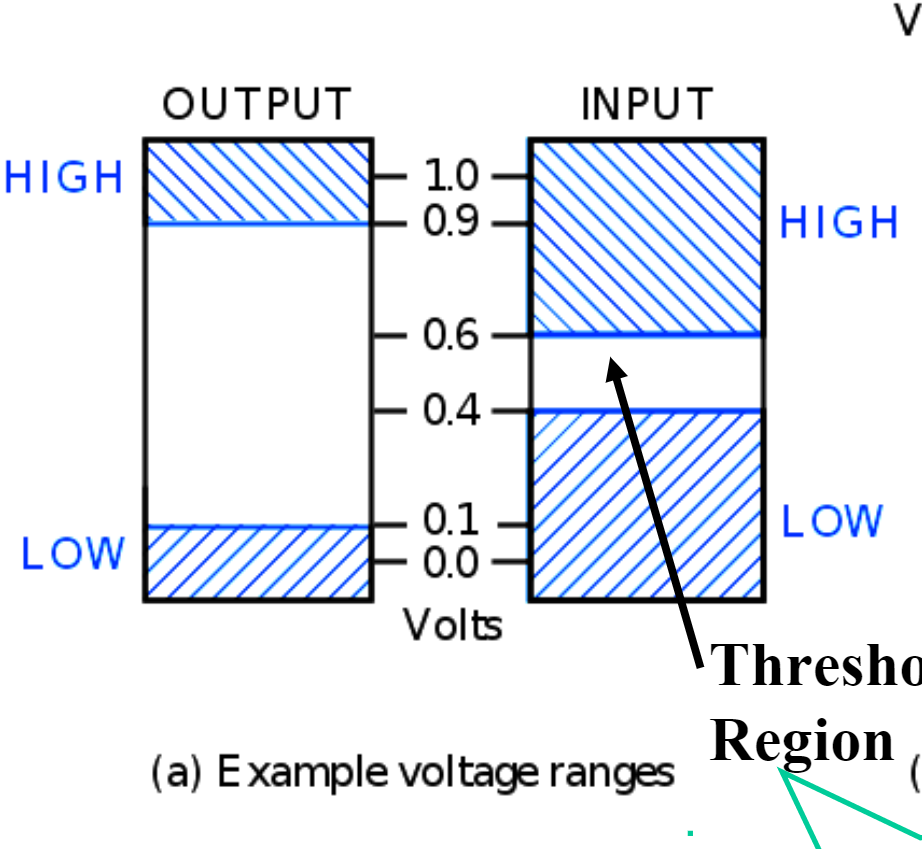
噪声容限 0.3V(0.6-0.9 0.1-0.4之间可以继续保留信息的正确性)

Number Systems¶

首先来看进制转换：

计算机中常见进制为 二进制(binary)，八进制(octal)，十进制(decimal)和十六进制(hexadecimal)

通常一个 \(r\) 进制数可以表示如下: \(A_{n-1}A_{n-2}\cdots A_1A_0.A_{-1}A_{-2}\dots A_{-m}\)

其对应的十进制数换算为：

\(Number_r = (\sum\limits_{i=0}^{i=n-1}A_i\times r^i)+(\sum\limits_{j=-m}^{j=-1}A_j\times r^j)\)

整数与小数分开转换

小数转换

十进制转化为\(x\)进制：小数部分乘\(x\)取整，余下小数部分重复此步骤至结束

2转8/16进制: 小数点向两边每次取3/4位，不够则补零

注意

十进制小数转换难免除不尽，要根据要求精度保留。
补零：
- 整数部分补零在左侧（不补没影响）
- 而小数部分补 0 是在右侧(最后)
  \((11 111 101. 010 011 110)_2 \neq (375.233)_8\) 最后要补 0, 应为 \((375.236)_8\)

Info

\(2^{10} = 1024\) is Kilo, denoted "K".
\(2^{20}\) is Mega, denoted "M".
\(2^{30}\) is Giga, denoted "G".
\(2^{40}\) is Tera, denoted "T".

Binary Arithmetic （二进制运算）¶

二进制加法: 全加器

二进制减法：注意0-1=11；计算机中依靠补码实现

二进制乘法: 根据乘数对应位是 1 还是 0, 如果是 1 就移位并加起来.(和十进制乘法没区别)

Binary Coding(二进制编码)¶

一个数值对应一个符号（例如交通信号灯）

主要有下面几种：

Numeric
- 必须表达一定范围内的数字；
- 支持简单且普遍的计算；
- 和二进制数本身关联较大
Non-numeric
- 相对灵活，亦即不需与普遍的运算法则相适配
  - 只要编码映射关系唯一就是合法编码
- 与二进制数本身未必有关系

给定M个符号，求至少需要的二进制位数n:

\(2^n>=M>2^{n-1}\) so \(n=\lceil{log_2{M}}\rceil\).

"one-hot" code(独热编码):M个符号，M个二进制位,有且仅有一位是1(对应独冷，只有一位是0)

(例如red_001;green_010;yellow_100)

Extra

使用这种编码的好处是，决定或改变状态机目前的状态的成本相对较低，容易设计也容易检测非法行为等。

但是相对应的，缺点是信息表示率较低，非法状态非常多而有效状态很少。

常见对十进制的十个数字进行编码:

Warning

BCD码和进制转换不同

13 = D = 1101(进制转化), 但在编码时会表示成 0001 0011(BCD码), 我们应该分别编码每个数字.

BCD Codes(Binary Code Decimal)¶

有权编码，每个码都有位权

可以计算，但要修正。（超过 9 要加 6）

Example

为什么需要 BCD 编码

电子表中有时针秒, 我们如果用二进制保存时针秒, 那么加到9以上得到 ABCD..., 当我们想要显示这些值时, 我们要先做进制转换, 再显示(如 A 转为 10) 这其中要做除法, 成本高.
但我们用两位 BCD 码表示, 就可以直接显示结果了.

Excess3(余三码)¶

8421 + 3 得到 Excess3 的值.

编码成对出现, i 和 9 - i 各位互反. 在通信时很有用处.

“3”来自于BCD码中加法修正时的\(\frac{16-10}{2}\),从而很好地解决了BCD加法中的进位问题

ASCII Codes¶

常用的 ASCII Code:

0 <-> \(30_{16}\)
A <-> \(41_{16}\) to \(5A_{16}\)
a <-> \(61_{16}\) to \(7A_{16}\)
Delete (DEL) is all bits set.

Parity Bit Error-Detection Codes(奇偶校验位)¶

信号传输过程中可能由于各种原因出现信号抖动，为保证数据可信度，需要一个错误检测机制。

一种常见方法是冗余，即加入一些额外的信息用来校验

一种做法是引入 奇偶校验位（Parity Bit）. 它分为：

偶校验：A code word has even parity if the number of 1’s in the code word is even.
奇校验：A code word has odd parity if the number of 1’s in the code word is odd.

添加一位，表示编码的奇偶性。

对偶校验来说，当1的个数为偶数时校验位为0.(如0101添加一位0成为01010)

对奇校验来说，当1的个数为奇数时校验位为1(如1101添加一位1成为11011)

此时若传输过程中出现问题，1的数量很可能变成奇数，从而得知此信息不对。

Gray Codes¶

应用: 光学传感器

编码器盘包含不透明区域和透明区域。
Opaque表示0 ,clear表示1。光通过编码器的每一个环，与编码的一个位相对应，照射在传感器上，产生一个0或1

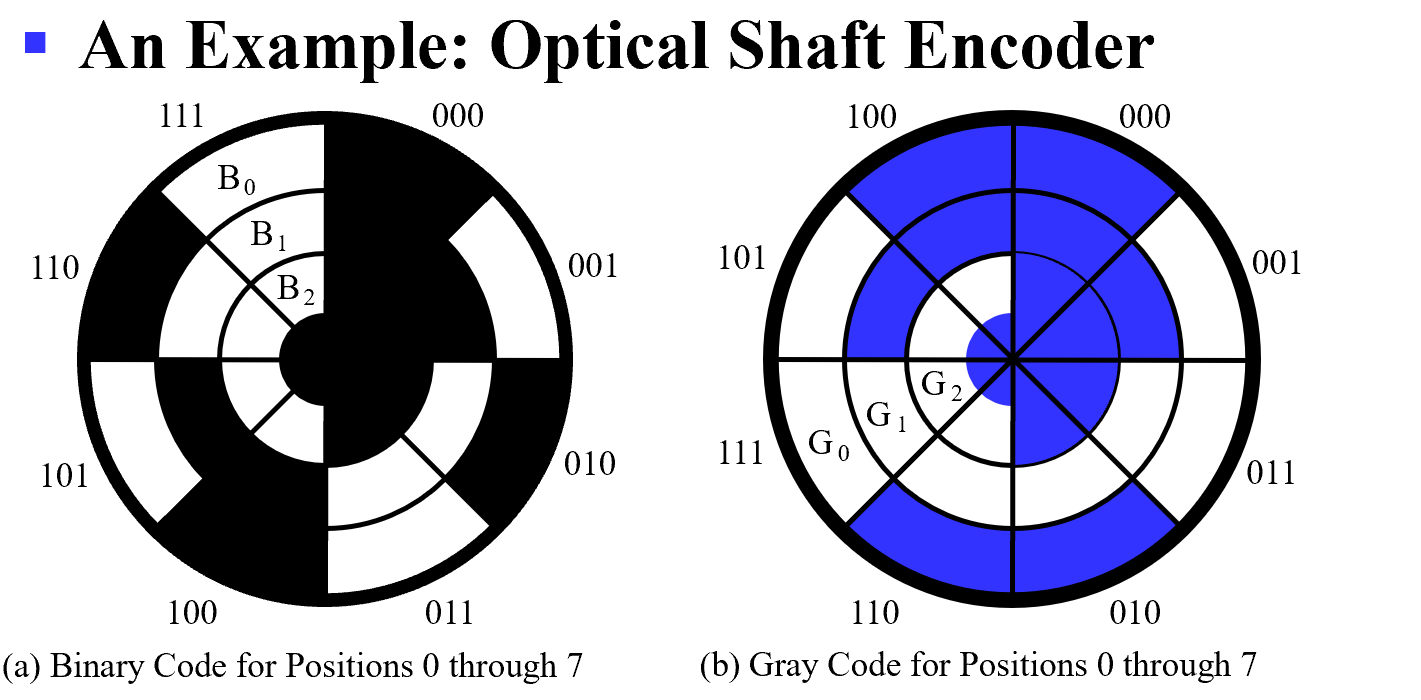
角编码器, 测量转轴转向的角度.
三个传感器不会在同一条直线(安装误差), 存在中间状况.
但格雷编码盘, 相邻编码只差一位, 对结果不会带来影响.

例如二进制编码 011 转换到 100 ，还有可能出现中间状态 000, 001, 010, 110, 101, 111; 但格雷编码只会是011或100。

Extra

格雷码的一种简单粗暴的写法，是通过「镜像」的技巧来倍增已知的格雷编码。

具体来说，如果现在有0 - 3的格雷码，分别是 00，01，11，10，那么我们可以将其增添一位前导 0，然后镜面对称地书写出带有前导 1 的4 - 7的格雷码。

最终我们得到的0 - 7的格雷码是：000，001，011，010，110，111，101，100

Unicode¶

Unicode extends ASCII to 65536(ASCII 最多只有 7 个二进制位, 后扩展为 8 个)

2 bytes(16 bits) code words
可以用来编码中文/韩文...等字符(ASCII 只能处理英文字母)

最后更新: 2024年3月18日 09:10:56
创建日期: 2024年3月9日 08:53:42